因應撰文這天正巧是中秋節來寫個應景的程式算法問題,
先快速公佈一下昨日課後練習解答:
def judge(scores):
return sorted(scores)[1:-1]
恭喜邦友ccutmis答對哦。
「小馬月餅店」開張囉,
為了吸引客人,
老闆想出了以下小遊戲與客人互動,
以決定月餅的價錢。
假設客人想買裝有n個月餅的禮盒一盒(n至少為2),
客人必須將n個月餅分成兩堆,
每堆至少一個月餅,
並將兩堆月餅的個數相乘,
得到第一個乘數。
之後再將第一堆和第二堆分別分成兩堆,
又會得到兩個乘數。
依此繼續下去,每堆僅剩一個月餅為止。
最後n個月餅的售價就是這些乘數的和。
舉例來說,假設n=5,
底下是小明的一種分堆方法: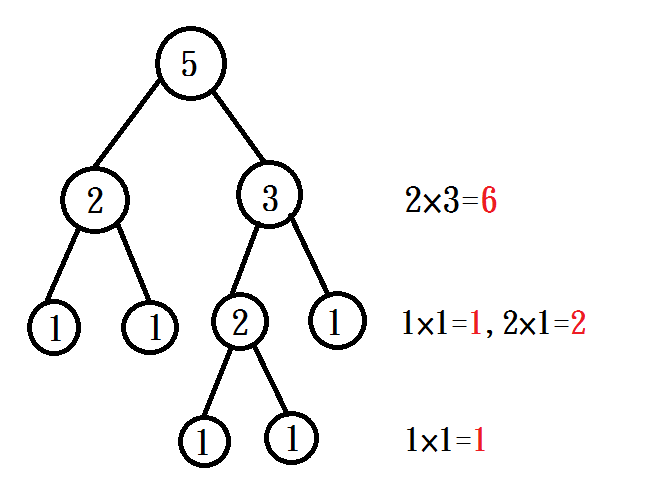
(圖示意思為先把5個月餅分成2、3兩堆,再各自把月餅繼續分堆)
因此,小明買五個月餅的錢數就是6 + 1 + 2 + 1 = 10塊錢。
請你實作一支程式,
計算小明需要買n個月餅最省錢的分堆分法的金額為何?
在此我提供一種思路:
既然不知道怎麼分月餅最好,
那先隨便亂分試試看好了。
先行介紹新工具教大家使用囉。
要產生隨機數,首先要在你的python程式裡加入這行:
import random
底下介紹常用的random函數
| 函數 | 說明 |
|---|---|
| random.randrange(start, stop[, step]) | 隨機回傳一個 range(start, stop, step) 之中的數值 |
| random.randint(a, b) | 隨機回傳一個整數 N (a <= N <= b) |
| random.random() | 隨機回傳一個浮點數 f (0 <= f <= 1) |
| random.uniform(a, b) | 隨機回傳一個浮點數 f (a <= f <= b) |
| random.choice(seq) | 隨機回傳seq裡的元素 |
| random.shuffle(seq) | 隨機洗亂seq裡的順序 |
這類random模組類的函數很特別,
一般來說,我們使用函數都是只要參數相同,那麼回傳的結果就是固定的,
試想你今天想計算pow(2,3)的值好了,也就是2的3次方,
那麼這個值你不管計算多少次,答案永遠是8。
但是這類隨機函數你每次調用的答案並不會每次都相同,
例如產生5個介於1到2之間的浮點數:
for i in range(5):
print(random.uniform(1,2))
可能印出:1.71577988434664161.00919359905626481.27210254406456351.78633414973119331.7895073195027238
(每個人電腦上執行的結果不同)
你可能說這類隨機函數可以用在哪裡?
它的用途可廣了,
許多遊戲元素都帶有隨機性,
例如: 骰子、撲克牌、猜拳啦
你可以運用random模組幫你模擬丟骰子的狀況,
也可以拿來模擬洗牌,
這邊暫不贅述。
回到原問題,我們也可以用random模組模擬隨意將月餅分堆的狀況,
雖然這方法看起來很蠢,
但說不定能幫助我們找到規律,
進而發現更漂亮的解法。
首先我們先定義 divMoonCakes這樣一個函式,
參數n表示有n個月餅,如下:
import random
def divMoonCakes(n):
mooncakes = [n]
其中,我們在函數內定義變數mooncakes = [n],
收集所有大於一個的月餅堆,
設定初始值只有一堆n個月餅。
想要把月餅分堆的邏輯我們可以這樣寫:
while mooncakes裡還有月餅:
隨意取出一堆月餅
將它分成更小的兩堆
把大於1個月餅的月餅堆放進列表mooncakes
把它寫成程式碼變成這樣:
import random
def divMoonCakes(n):
mooncakes = [n]
while mooncakes:
m = random.choice(mooncakes)
mooncakes.remove(m)
div = random.randint(1,m-1)
if div!=1:
mooncakes.append(div)
if m-div!=1:
mooncakes.append(m-div)
為了清楚看到分月餅的過程,我們加幾個print()函數印出資訊:
def divMoonCakes(n):
mooncakes = [n]
while mooncakes:
m = random.choice(mooncakes)
mooncakes.remove(m)
print("取出"+str(m)+"個月餅")
div = random.randint(1,m-1)
print(f"把{m}個月餅分成{div}和{m-div}兩堆")
if div!=1:
mooncakes.append(div)
if m-div!=1:
mooncakes.append(m-div)
print("目前待分月餅堆: ", mooncakes)
(哦,對了,你可能沒看過在字串前加f的語法,
如f"把{m}個月餅分成{div}和{m-div}兩堆"這句,
這是在python3.6版的新特性,
可以很方便的在字串內放入變數)
我們實際執行程式試試吧:
>>> divMoonCakes(5)
取出5個月餅
把5個月餅分成2和3兩堆
目前待分月餅堆: [2, 3]
取出2個月餅
把2個月餅分成1和1兩堆
目前待分月餅堆: [3]
取出3個月餅
把3個月餅分成1和2兩堆
目前待分月餅堆: [2]
取出2個月餅
把2個月餅分成1和1兩堆
目前待分月餅堆: []
可以看到目前已經可以印出月餅分堆的過程了
(由於用了隨機函數,每次分堆的過程會不一樣)
計得原題目是要計算買n個月餅「最省錢」的方法。
我們增加一個變數money,
用來統計月餅的總價,
並在每次分月餅的時候增加money的值。
程式更改如下:
def divMoonCakes(n):
mooncakes = [n]
money = 0
print(f"月餅小計 {money} 元")
while mooncakes:
m = random.choice(mooncakes)
mooncakes.remove(m)
print("取出"+str(m)+"個月餅")
div = random.randint(1,m-1)
print(f"把{m}個月餅分成{div}和{m-div}兩堆,總共增加{div*(m-div)}元")
money += div*(m-div)
print(f"目前月餅小計 {money} 元")
if div!=1:
mooncakes.append(div)
if m-div!=1:
mooncakes.append(m-div)
print("目前待分月餅堆: ", mooncakes)
return money
再試著執行一次程式試試吧:
>>> divMoonCakes(5)
月餅小計 0 元
取出5個月餅
把5個月餅分成3和2兩堆,總共增加6元
目前月餅小計 6 元
目前待分月餅堆: [3, 2]
取出2個月餅
把2個月餅分成1和1兩堆,總共增加1元
目前月餅小計 7 元
目前待分月餅堆: [3]
取出3個月餅
把3個月餅分成1和2兩堆,總共增加2元
目前月餅小計 9 元
目前待分月餅堆: [2]
取出2個月餅
把2個月餅分成1和1兩堆,總共增加1元
目前月餅小計 10 元
目前待分月餅堆: []
好的,目前已經可以算出月餅總價了。
目前得到五個月餅是10元
我們再執行一次程式看看:
>>> divMoonCakes(5)
月餅小計 0 元
取出5個月餅
把5個月餅分成4和1兩堆,總共增加4元
目前月餅小計 4 元
目前待分月餅堆: [4]
取出4個月餅
把4個月餅分成2和2兩堆,總共增加4元
目前月餅小計 8 元
目前待分月餅堆: [2, 2]
取出2個月餅
把2個月餅分成1和1兩堆,總共增加1元
目前月餅小計 9 元
目前待分月餅堆: [2]
取出2個月餅
把2個月餅分成1和1兩堆,總共增加1元
目前月餅小計 10 元
目前待分月餅堆: []
這次分堆方式確實不一樣了,
結果五個月餅還是10元。
事實上不論你執行幾次,算出來的結果一定都是10元。
是巧合嗎?
會不會是5這個數字太小,
分堆方式不夠多,所以才會這樣呢?
我們換成10個月餅試試,
為了避免把過程印出來太占版面,
我先把函數內印出的資訊註解掉,
並用for迴圈執行10次看看。
for i in range(10):
print(f"10個月餅總計{divMoonCakes(10)}元")
結果十次都是10個月餅總計45元
雖說十個月餅的分堆分法有這種多種,
但是不論怎麼分竟都得到相同結果,
似乎很難想像這是巧合。
其實我們可以合理猜測:
當n固定時,買n個月餅的價格也是固定的,
只是目前不知原因。
好吧,現在改變參數n,
再執行一次觀察看看規律吧,
for n in range(2, 11):
print(f"{n}個月餅總計{divMoonCakes(n)}元")
得到這樣的結果:
2個月餅總計1元
3個月餅總計3元
4個月餅總計6元
5個月餅總計10元
6個月餅總計15元
7個月餅總計21元
8個月餅總計28元
9個月餅總計36元
10個月餅總計45元
發現似乎有某種規律。
其實數學上可以證明,n個月餅的價錢總和恰為
def priceOfMooncakes(n):
return sum(range(1,n))

for n in range(11):
print(f"{n}個月餅總計{divMoonCakes(n)}元")
結果出現n從2開始,是不是要改成range(2,11)
月餅的問題很有趣,還沒看程式碼之前,我也用列舉法得到價錢為n(n-1)/2
n個月餅分堆,可以每次都分成1和其他
(1,n-1)
(1,n-2)
...
(1,1)
價錢 = 1n-1 + 1n-2 + ... + 1*1 = 1~n-1的和
因為列舉每次價錢都一樣,假設價錢n(n-1)/2
用類似遞迴的方式證明
假設n個月餅分成a和n-a個,其中1<=a<=n-1
價錢公式是對的若且唯若n(n-1)/2 = a(n-a) + a(a-1)/2 + (n-a)(n-a-1)/2
運算後成立,得證